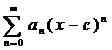Perbezaan Antara Siri Kuasa dan Siri Taylor

Siri Kuasa vs Taylor Series

Dalam matematik, urutan sebenar adalah senarai nombor sebenar yang diperintahkan. Secara rasmi, ia adalah fungsi dari set nombor semula jadi ke set nombor sebenar. Jika a_nadalah n^th istilah urutan, kami menandakan urutan oleh atau oleh a₁, a₂,..., a_n,… .Sebagai contoh, pertimbangkan urutan 1, ½, ⅓, .. , ¹/_n,… . Ia boleh dilambangkan sebagai 1/n.

Adalah mungkin untuk menentukan siri menggunakan urutan. Satu siri adalah jumlah syarat urutan. Oleh itu, bagi setiap urutan, terdapat urutan yang berkaitan dan sebaliknya. Sekiranya_n adalah urutan yang dipertimbangkan, maka siri yang dibentuk oleh urutan itu boleh diwakili sebagai:                                           

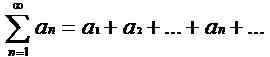
 Oleh itu, dalam contoh di atas, siri yang berkaitan ialah 1+¹/₂+¹/₃+…  + ¹/_n +… . 

Seperti yang dicadangkan oleh nama, siri kuasa adalah jenis siri khas dan ia digunakan secara meluas dalam analisis berangka dan pemodelan matematik yang berkaitan. Taylor Series adalah siri kuasa khas yang menyediakan cara alternatif dan mudah untuk mewakili fungsi yang terkenal.

Apa itu Siri Kuasa?

Siri Kuasa adalah satu siri borang

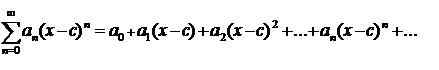
yang konvergen (mungkin) untuk beberapa selang berpusat di c. Koefisien a_n boleh menjadi nombor sebenar atau kompleks, dan bebas dari x; i.e. pembolehubah dummy.

Contohnya, dengan menetapkan a_n= 1 untuk masing -masing n, dan c = 0, Siri Kuasa 1+x+x²+... + xⁿ+... diperolehi. Sangat mudah untuk memerhatikan bahawa apabila x ε (-1,1), siri kuasa ini menumpu kepada 1/(1-x).          

Siri kuasa menumpu ketika x = c. Nilai lain dari x yang mana siri kuasa berkumpul akan sentiasa mengambil bentuk selang terbuka yang berpusat di c. Itu dia, akan ada nilai 0≤ R ≤ ∞ seperti itu untuk masing -masing x memuaskan | x-c | ≤R, siri kuasa adalah konvergen dan untuk masing -masing x  memuaskan | x-c |>R, siri kuasa berbeza. Nilai ini R dipanggil jejari konvergensi siri kuasa (R boleh mengambil nilai sebenar atau infiniti positif).

Siri Kuasa boleh ditambah, ditolak, didarab dan dibahagikan dengan menggunakan peraturan berikut. Pertimbangkan dua siri kuasa:       

                               .

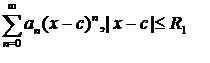
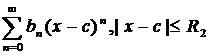Kemudian,                 

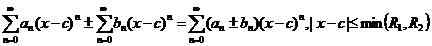
i.e. Suka istilah ditambah atau dikurangkan bersama. Juga, ada kemungkinan untuk membiak dan membahagikan dua siri kuasa menggunakan identiti,

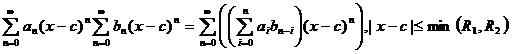
Apa itu siri Taylor?

Siri Taylor ditakrifkan untuk fungsi f(x) yang sangat berbeza pada selang waktu. Anggap f(x) boleh dibezakan pada selang yang berpusat pada c. Kemudian siri kuasa yang diberikan oleh

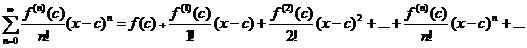
dipanggil pengembangan siri Taylor fungsi f(x) mengenai c. (Di sini f⁽ⁿ⁾(c) Menunjukkan n^th Derivatif pada x = c). Dalam analisis berangka, bilangan istilah terhingga dalam pengembangan tak terhingga ini digunakan dalam mengira nilai pada titik di mana siri ini bersatu dengan fungsi asal.

Fungsi f(x) dikatakan analitik dalam selang waktu (a, b), jika bagi setiap x ε (a, b), siri Taylor dari f(x) menumpu ke fungsi f(x). Sebagai contoh, 1/(1-x) adalah analitik pada (-1,1), kerana pengembangan Taylor 1+x+x²+... + xⁿ+... menumpu ke fungsi pada selang itu, dan e^x  adalah analitik di mana -mana, kerana siri Taylor e^xberkumpul ke e^x untuk setiap nombor sebenar x.

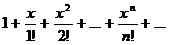
Apakah Perbezaan Antara Siri Kuasa dan Siri Taylor?

1. Siri Taylor adalah kelas khas siri kuasa yang ditakrifkan hanya untuk fungsi yang tidak dapat dibezakan pada beberapa selang terbuka.

2. Siri Taylor mengambil bentuk khas

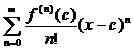
sedangkan, siri kuasa boleh menjadi siri borang