Perbezaan antara matriks transpose dan songsang

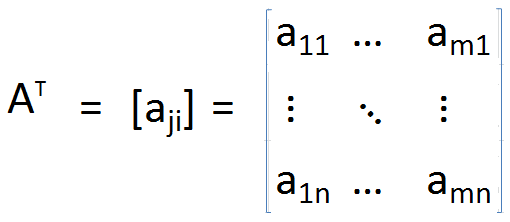
Transpose vs matriks songsang
 

Transpose dan songsang adalah dua jenis matriks dengan sifat khas yang kita hadapi dalam aljabar matriks. Mereka berbeza antara satu sama lain, dan tidak berkongsi hubungan yang erat kerana operasi yang dilakukan untuk mendapatkannya berbeza.

Mereka mempunyai aplikasi yang luas dalam bidang aljabar linear dan pelaksanaan yang diperolehi seperti sains komputer.

Lebih lanjut mengenai matriks transpose

Transpose matriks A boleh dikenal pasti sebagai matriks yang diperolehi dengan menyusun semula lajur sebagai baris atau baris sebagai lajur. Akibatnya, indeks setiap elemen ditukar. Lebih formal, transpose matriks A, ditakrifkan sebagai

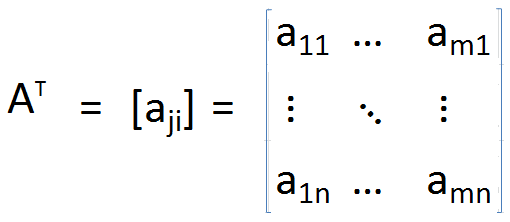
di mana

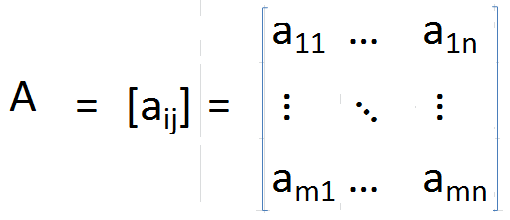
Dalam matriks transpose, pepenjuru tetap tidak berubah, tetapi semua elemen lain diputar di sekitar pepenjuru. Juga, saiz matriks juga berubah dari m × n hingga n × m.

Transpose mempunyai beberapa sifat penting, dan mereka membenarkan manipulasi matriks yang lebih mudah. Juga, beberapa matriks transpose penting ditakrifkan berdasarkan ciri -ciri mereka. Sekiranya matriks sama dengan transposanya, maka matriks adalah simetri. Sekiranya matriks sama dengan negatif transpose, matriks adalah simetri condong. Transpose conjugate matriks adalah transpose matriks dengan unsur -unsur digantikan dengan konjugasi kompleksnya.

Lebih banyak mengenai matriks songsang

Songsang matriks ditakrifkan sebagai matriks yang memberikan matriks identiti apabila didarabkan bersama. Oleh itu, dengan definisi, jika Ab = ba = i kemudian B adalah matriks songsang dari A dan A adalah matriks songsang dari B. Jadi, jika kita mempertimbangkan B = A^-1 , kemudian Aa^-1 = A^-1A = i

Untuk matriks dapat terbalik, keadaan yang perlu dan mencukupi ialah penentu A tidak sifar; i.E |A| = det (A) ≠ 0. Matriks dikatakan boleh terbalik, tidak berselisih, atau tidak diseliru jika ia memenuhi syarat ini. Ia mengikutinya A adalah matriks persegi dan kedua -duanya A^-1 dan A mempunyai saiz yang sama.

Kebalikan dari matriks A Boleh dikira dengan banyak kaedah dalam aljabar linear seperti penghapusan Gaussian, eigendecomposition, penguraian cholesky, dan peraturan Carmer. Matriks juga boleh terbalik dengan kaedah penyongsangan blok dan siri Neuman.

Apakah perbezaan antara matriks transpose dan songsang?

• Transpose diperoleh dengan menyusun semula lajur dan baris dalam matriks sementara songsang diperolehi dengan pengiraan berangka yang agak sukar. (Tetapi pada hakikatnya kedua -duanya adalah transformasi linear)

• Sebagai hasil langsung, unsur -unsur dalam transpose hanya mengubah kedudukan mereka, tetapi nilai adalah sama. Tetapi dalam songsang, nombor boleh sama sekali berbeza dari matriks asal.

• Setiap matriks boleh mempunyai transpose, tetapi songsang hanya ditakrifkan untuk matriks persegi, dan penentu harus menjadi penentu bukan sifar.