Perbezaan antara lilitan, diameter dan jejari

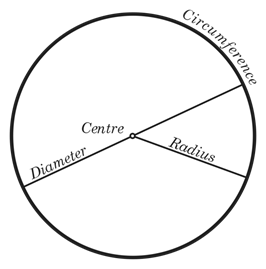
Lilitan vs diameter vs jejari
 

Radius, diameter, dan lilitan adalah pengukuran tiga sifat penting dalam bulatan.

Diameter dan jejari

Bulatan ditakrifkan sebagai lokus titik pada jarak tetap dari titik tetap pada satah dua dimensi. Titik tetap dikenali sebagai pusat. Panjang tetap dikenali sebagai jejari. Ia adalah jarak terpendek antara pusat dan lokus. Segmen garis bermula dari lokus yang melalui pusat dan berakhir di lokus dikenali sebagai diameter.

Radius dan diameter adalah parameter penting bulatan kerana mereka menentukan saiz bulatan. Untuk melukis bulatan, sama ada radius atau diameter hanya diperlukan.

Diameter dan jejari secara matematik berkaitan dengan formula berikut

D = 2r

di mana D adalah diameter dan r ialah jejari.

Lilitan

Lokus titik dikenali sebagai lilitan. Lilitan adalah garis melengkung, dan panjangnya bergantung pada jejari atau diameter. Hubungan matematik antara jejari (atau diameter) dan lilitan diberikan oleh formula berikut:

C = 2πr = πd

Di mana C Adakah lilitan dan π = 3.14. Surat Yunani pi (π) adalah tetap dan penting dalam banyak sistem matematik dan fizikal. Ia adalah nombor yang tidak rasional dan mempunyai nilai 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825.e. π = 3.14, cukup untuk ketepatan yang cukup.

Selalunya, dalam matematik sekolah peringkat pertengahan, di atas formula digunakan untuk menentukan pemalar pi (π) sebagai nisbah antara diameter bulatan dan lilitannya, di mana nilainya kira -kira diberikan sebagai pecahan 22/7.

Apakah perbezaan antara lilitan, jejari, dan diameter?

• Radius dan diameter adalah garis lurus manakala lilitan adalah lengkung tertutup.

• diameter dua kali ganda jejari.

• Lingkaran adalah 2π kali jejari bulatan atau π kali diameter bulatan.