Perbezaan antara kumpulan titik dan kumpulan ruang angkasa
Perbezaan utama - Kumpulan Point vs Ruang Kumpulan
Kumpulan Titik Terma dan Kumpulan Angkasa digunakan dalam Crystallography. Crystallography adalah kajian susunan atom dalam pepejal kristal. Kumpulan titik crystallographic adalah satu set operasi simetri yang meninggalkan sekurang -kurangnya satu titik yang tidak disengajakan. Operasi simetri adalah tindakan mendapatkan imej asal objek walaupun setelah memindahkannya. Operasi simetri yang digunakan dalam kumpulan titik adalah putaran dan pantulan. Kumpulan Angkasa adalah kumpulan simetri 3D konfigurasi di ruang angkasa. Kumpulan simetri adalah kumpulan semua transformasi yang diperoleh tanpa mengubah komposisi semasa operasi kumpulan. The Perbezaan utama antara kumpulan titik dan kumpulan ruang adalah Terdapat 32 kumpulan titik kristalografi manakala terdapat 230 kumpulan ruang yang dicipta oleh kombinasi 32 mata kumpulan dan 14 kisi bravais.
Kandungan
1. Gambaran Keseluruhan dan Perbezaan Utama
2. Apa itu Kumpulan Point
3. Apa itu Kumpulan Angkasa
4. Perbandingan sampingan - Kumpulan Point Vs Space dalam bentuk jadual
5. Ringkasan
Apa itu Kumpulan Point?
Kumpulan titik crystallographic adalah satu set operasi simetri yang meninggalkan sekurang -kurangnya satu titik yang tidak disengajakan. Operasi simetri yang diterangkan dalam kumpulan titik adalah putaran dan pantulan. Dalam Operasi Simetri Kumpulan Point, satu titik pusat dalam objek disimpan tidak tercemar (tetap) sambil menggerakkan wajah lain objek ke kedudukan ciri -ciri yang sama. Di sana, ciri makroskopik objek harus tetap sama sebelum dan selepas operasi simetri.
Untuk mana -mana objek yang diberikan, terdapat beberapa operasi simetri tertentu yang mungkin (dengan hubungan geometri yang ditetapkan di kalangan operasi simetri). Objek dikatakan mempunyai simetri yang diterangkan oleh kumpulan titik. Oleh itu, objek yang berbeza yang mempunyai simetri titik yang berbeza digambarkan oleh kumpulan titik yang berbeza.
Dalam notasi kumpulan titik, terdapat dua sistem yang digunakan;
-
Notasi Schoenflies
Dalam sistem notasi Schoenflies, kumpulan titik dinamakan sebagai cnv, CNH, DNH, Td, Oh, dan lain-lain. Simbol yang berbeza yang digunakan dalam sistem notasi ini diberikan di bawah.
- n ialah bilangan paksi putaran tertinggi
- v adalah satah cermin menegak (disebut hanya apabila tiada pesawat cermin mendatar)
- H adalah pesawat cermin mendatar
- T adalah kumpulan titik tetrahedral
- adalah kumpulan titik octahedral
Contohnya, cn digunakan menunjukkan bahawa kumpulan titik mempunyai paksi putaran n-lipat. Apabila ia diberikan sebagai cNH, itu bermaksud ada cn Bersama dengan satah cermin (satah refleksi) serenjang dengan paksi putaran. Sebaliknya, cnv adalah cn dengan pesawat cermin selari dengan paksi putaran. Sekiranya kumpulan titik diberikan sebagai s2n, ia menunjukkan bahawa kumpulan titik hanya mempunyai paksi refleksi putaran 2n kali ganda.
-
Notasi Hermann-Mauguin
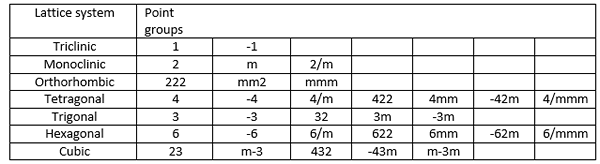
Sistem notasi Hermann-Mauguin biasanya digunakan untuk kumpulan ruang angkasa. Tetapi, ia juga digunakan untuk kumpulan titik kristal. Ia memberikan paksi putaran tertinggi. Contohnya, kumpulan titik yang hanya mempunyai paksi putaran 2 kali ganda dilambangkan sebagai 2. Kumpulan titik diberikan sebagai c2h oleh notasi schoenflies diberikan sebagai 2/m dalam sistem notasi Hermann-mauguin di mana simbol 'm' menunjukkan satah cermin dan simbol slash menunjukkan bahawa satah cermin berserenjang dengan paksi dua kali ganda. Jadual berikut menunjukkan nota kumpulan titik yang berbeza untuk sistem kekisi yang berbeza.

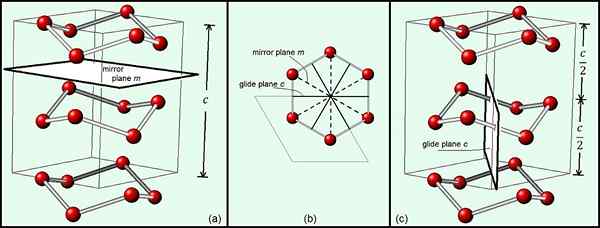
Rajah 01: Pesawat cermin dan pesawat meluncur ais heksagon menunjukkan bahawa kumpulan ruang ais adalah p63/mmc
Terdapat 32 kumpulan mata. Kumpulan titik paling mudah ialah 1, 2, 3, 4, 5 dan 6. Semua kumpulan titik ini hanya terdiri daripada satu paksi putaran. Untuk inversi Rotary, terdapat paksi bernama -1, m, -3, -4 dan -6. Kumpulan 22 titik lain adalah kombinasi kumpulan titik ini.
Apa itu Kumpulan Angkasa?
Kumpulan Angkasa adalah kumpulan simetri 3D konfigurasi di ruang angkasa. Terdapat 230 kumpulan ruang angkasa. 230 kumpulan ini adalah gabungan 32 kumpulan titik kristal (disebutkan di atas) dan 14 kisi Bravais. The Latihan Bravais diberikan dalam jadual di bawah.
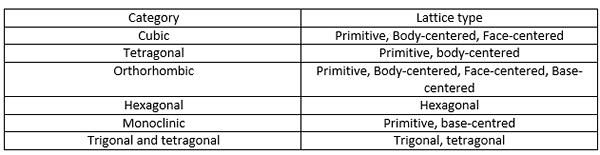
Kumpulan Angkasa memberikan keterangan mengenai simetri kristal. Kumpulan Ruang adalah kombinasi simetri translasi sel unit dan operasi simetri seperti putaran, rotary-inversion, refleksi, paksi skru dan operasi simetri pesawat meluncur.
Apakah perbezaan antara kumpulan titik dan kumpulan ruang angkasa?
Point Group vs Space Group | |
| Kumpulan titik crystallographic adalah satu set operasi simetri yang meninggalkan sekurang -kurangnya satu titik yang tidak disengajakan. | Kumpulan Angkasa adalah kumpulan simetri 3D konfigurasi di ruang angkasa. |
| Komponen | |
| Terdapat 32 kumpulan titik kristal. | Terdapat 230 Kumpulan Angkasa (dicipta oleh gabungan 32 kumpulan mata dan 14 kisi Bravais). |
| Operasi simetri | |
| Operasi simetri yang digunakan dalam pengesanan kumpulan titik adalah putaran dan refleksi. | Operasi simetri yang digunakan dalam pengesanan kumpulan ruang adalah putaran, rotary-inversion, refleksi, paksi skru dan operasi simetri pesawat meluncur. |
Ringkasan - Kumpulan titik vs Ruang Kumpulan
Kumpulan titik dan kumpulan ruang adalah istilah yang diterangkan di bawah kristalografi. Kumpulan titik crystallographic adalah satu set operasi simetri yang semuanya meninggalkan sekurang -kurangnya satu titik yang tidak disengajakan. Kumpulan Angkasa adalah kumpulan simetri 3D konfigurasi di ruang angkasa. Perbezaan antara kumpulan titik dan kumpulan ruang adalah bahawa terdapat 32 kumpulan titik kristalografi manakala terdapat 230 kumpulan ruang (dicipta oleh gabungan 32 mata kumpulan dan 14 kisi Bravais).
Rujukan:
1."2: Operasi simetri dan elemen simetri."Kimia Libretexts, Libretexts, 6 Mei 2017. Terdapat di sini
2."Kumpulan titik kristalografi."Wikipedia, Yayasan Wikimedia, 28 Feb. 2018. Terdapat di sini
Ihsan gambar:
1.'Ice IH Space Group'By Dbuckingham42 - Kerja Sendiri, (CC BY -SA 4.0) melalui Commons Wikimedia


