Perbezaan antara integrasi dan penjumlahan

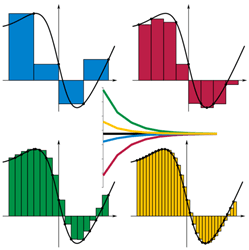
Integrasi vs penjumlahan
 

Di atas matematik sekolah menengah, integrasi dan penjumlahan sering dijumpai dalam operasi matematik. Mereka kelihatannya digunakan sebagai alat yang berbeza dan dalam situasi yang berbeza, tetapi mereka berkongsi hubungan yang sangat dekat.

Lebih banyak mengenai penjumlahan

Summation adalah operasi menambahkan urutan nombor dan operasi sering dilambangkan oleh huruf Yunani Sigma Modal σ. Ia digunakan untuk menyingkat penjumlahan dan sama dengan jumlah/jumlah urutan. Mereka sering digunakan untuk mewakili siri ini, yang pada dasarnya adalah urutan tak terhingga yang disimpulkan. Mereka juga boleh digunakan untuk menunjukkan jumlah vektor, matriks, atau polinomial.

Penjumlahan biasanya dilakukan untuk pelbagai nilai yang boleh diwakili oleh istilah umum, seperti siri yang mempunyai istilah yang sama. Titik permulaan dan titik akhir penjumlahan dikenali sebagai terikat bawah dan terikat atas penjumlahan, masing -masing.

Sebagai contoh, jumlah urutan a₁, a₂, a₃, a₄, ..., a_n ialah₁ + a₂ + a₃ +... + a_n yang boleh diwakili dengan mudah menggunakan notasi penjumlahan sebagai Σⁿ_{i = 1} a_i; Saya dipanggil indeks penjumlahan.

Banyak variasi digunakan untuk penjumlahan berdasarkan aplikasi. Dalam sesetengah kes, terikat atas dan batas bawah boleh diberikan sebagai selang atau julat, seperti Σ_{1 ≤ ≤100} a_i dan Σ_{i∈ [1,100]} a_i. Atau ia boleh diberikan sebagai satu set nombor seperti Σ_i∈P a_i , di mana p adalah set yang ditetapkan.

Dalam sesetengah kes, dua atau lebih tanda Sigma boleh digunakan, tetapi mereka boleh umum seperti berikut; Σ_j Σ_k a_jk = Σ_{J, k} a_jk.

Juga, penjumlahan mengikuti banyak peraturan algebra. Oleh kerana operasi tertanam adalah penambahan, banyak peraturan biasa algebra boleh digunakan untuk jumlah itu sendiri dan untuk istilah individu yang digambarkan oleh penjumlahan.

Lebih banyak mengenai integrasi

Integrasi ditakrifkan sebagai proses pembezaan terbalik. Tetapi dalam pandangan geometri ia juga boleh dianggap sebagai kawasan yang dilampirkan oleh lengkung fungsi dan paksi. Oleh itu, pengiraan kawasan memberikan nilai integral yang pasti seperti yang ditunjukkan dalam rajah.

Sumber Imej: http: // en.Wikipedia.org/wiki/fail: riemann_sum_convergence.png

Nilai integral yang pasti sebenarnya adalah jumlah jalur kecil di dalam lengkung dan paksi. Kawasan setiap jalur adalah ketinggian × lebar pada titik pada paksi yang dipertimbangkan. Lebar adalah nilai yang boleh kita pilih, katakan Δx. Dan ketinggian adalah kira -kira nilai fungsi pada titik yang dipertimbangkan, katakan f(x_i). Dari gambarajah, jelas bahawa lebih kecil jalur lebih baik jalur sesuai di dalam kawasan yang dibatasi, oleh itu penghampiran yang lebih baik dari nilai.

Oleh itu, secara umumnya integral pasti I, antara mata a dan b (i.e dalam selang [a, b] di mana aI ≅ f(x₁) Δx + f(x₂) Δx + ⋯ + f(x_n) Δx, di mana n ialah bilangan jalur (n = (b-a)/Δx). Penjumlahan kawasan ini dapat dengan mudah diwakili menggunakan notasi penjumlahan sebagai I ≅ Σⁿ_{i = 1} f(x_i) Δx. Oleh kerana penghampiran lebih baik apabila Δx lebih kecil, kita dapat mengira nilai apabila Δx → 0. Oleh itu, adalah munasabah untuk mengatakan I = lim_{Δx → 0} Σⁿ_{i = 1} f(x_i) Δx.

Sebagai generalisasi dari konsep di atas, kita boleh memilih Δx berdasarkan selang yang dipertimbangkan diindeks oleh i (memilih lebar kawasan berdasarkan kedudukan). Kemudian kita dapat

I= lim_{Δx → 0} Σⁿ_{i = 1} f(x_i) Δx_i = _a∫^b f(x) dx

Ini dikenali sebagai integral reimann fungsi f(x) Dalam selang [a, b]. Dalam kes ini A dan B dikenali sebagai terikat atas dan terikat lebih rendah dari integral. Reimann Integral adalah bentuk asas semua kaedah integrasi.

Pada dasarnya, integrasi adalah penjumlahan kawasan apabila lebar segi empat tepat adalah tak terhingga.

Apakah perbezaan antara integrasi dan penjumlahan?

• penjumlahan menambah urutan nombor. Biasanya, penjumlahan diberikan dalam bentuk ini ∑ⁿ_{i = 1} a_i Apabila istilah dalam urutan mempunyai corak dan boleh dinyatakan menggunakan istilah umum.

• Integrasi pada dasarnya adalah kawasan yang dibatasi oleh lengkung fungsi, paksi dan had atas dan bawah. Kawasan ini boleh diberikan sebagai jumlah kawasan yang lebih kecil yang termasuk di kawasan yang dibatasi.

• Summasi melibatkan nilai diskret dengan batas atas dan bawah, sedangkan integrasi melibatkan nilai berterusan.

• Integrasi dapat ditafsirkan sebagai bentuk penjumlahan khas.

• Dalam kaedah pengiraan berangka, integrasi sentiasa dilakukan sebagai penjumlahan.