Perbezaan antara pengedaran binomial dan normal

Binomial vs taburan normal
 

Pengagihan kebarangkalian pembolehubah rawak memainkan peranan penting dalam bidang statistik. Daripada pengagihan kebarangkalian, pengedaran binomial dan pengedaran normal adalah dua yang paling biasa berlaku dalam kehidupan sebenar.

Apa itu pengedaran binomial?

Pengagihan binomial adalah taburan kebarangkalian yang sepadan dengan pemboleh ubah rawak X, yang merupakan bilangan kejayaan a Urutan terhingga eksperimen ya/tidak bebas yang masing -masing mempunyai kebarangkalian kejayaan p. Dari definisi X, Adalah jelas bahawa ia adalah pemboleh ubah rawak diskret; Oleh itu, pengedaran binomial juga diskret.

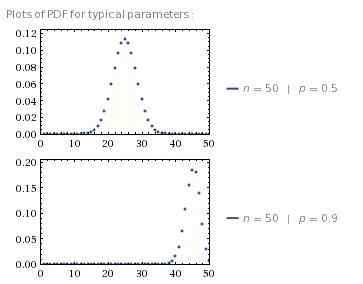
Pengagihan dilambangkan sebagai X ~B(n,p) di mana n adalah bilangan eksperimen dan p adalah kebarangkalian kejayaan. Mengikut teori kebarangkalian, kita dapat menyimpulkannya B(n,p) mengikuti fungsi massa kebarangkalian [lateks] b (n, p) \\ sim \\ binom n k p^k (1-p)^(n-k), k = 0, 1, 2, ... n [/lateks]. Dari persamaan ini, dapat disimpulkan lagi bahawa nilai yang diharapkan X, E (X) = np dan varians dari X, V (X) = np(1-p).

Sebagai contoh, pertimbangkan percubaan rawak untuk melemparkan duit syiling 3 kali. Tentukan kejayaan sebagai mendapatkan H, kegagalan sebagai mendapatkan t dan pemboleh ubah rawak X Seperti jumlah kejayaan dalam eksperimen. Kemudian X~B(3, 0.5) dan fungsi jisim kebarangkalian X Diberikan oleh [latex] \\ binom 3 k 0.5^k (0.5)^(3-k), k = 0, 1, 2.[/lateks]. Oleh itu, kebarangkalian mendapatkan sekurang -kurangnya 2 jam ialah P (X ≥ 2) = p (X = 2 atau X = 3) = p (X = 2) + p (X = 3) = ³C₂(0.5²) (0.5¹) + ³C₃(0.5³) (0.5⁰) = 0.375 + 0.125 = 0.5.

Apakah pengedaran biasa?

Pengagihan normal adalah taburan kebarangkalian berterusan yang ditakrifkan oleh fungsi ketumpatan kebarangkalian, [latex] n (\\ mu, \\ sigma) \\ sim \\ frac 1 \\ sqrt 2 \\ pi \\ sigma^ 2 \\ e^- \\ frac (x- \\ mu)^2 2 \\ sigma^2 [/lateks]. Parameter [lateks] \\ mu dan \\ sigma [/lateks] menunjukkan min dan sisihan piawai populasi kepentingan. Bila [lateks] \\ mu = 0 dan \\ sigma = 1 [/lateks] Pengagihan dipanggil taburan normal standard.

Pengagihan ini dipanggil normal kerana kebanyakan fenomena semulajadi mengikuti taburan normal. Contohnya, IQ penduduk manusia diedarkan secara normal. Seperti yang dilihat dari graf, ia tidak sama, simetri mengenai min dan loceng berbentuk. Maksud, mod, dan median bertepatan. Kawasan di bawah lengkung sepadan dengan bahagian penduduk, memenuhi syarat tertentu.

Bahagian penduduk dalam selang [lateks] (\\ mu - \\ sigma, \\ mu + \\ sigma) [/latex], [latex] (\\ mu - 2 \\ sigma, \\ mu + 2 \\ sigma) [/lateks], [lateks] (\\ mu - 3 \\ sigma, \\ mu + 3 \\ sigma) [/lateks].2%, 95.6% dan 99.8% masing -masing.

Apakah perbezaan antara pengagihan binomial dan biasa?

• Pengagihan binomial adalah taburan kebarangkalian diskret manakala pengedaran normal adalah satu yang berterusan.
• Fungsi jisim kebarangkalian pengedaran binomial adalah [lateks] b (n, p) \\ sim \\ binom n k p^k (1-p)^(n-k) [/lateks] , sedangkan fungsi ketumpatan kebarangkalian taburan normal adalah [lateks] n (\\ mu, \\ sigma) \\ sim \\ frac 1 \\ sqrt 2 \\ pi \\ sigma^2 \\ e^- \\ frac (x- \\ mu)^2 2 \\ sigma^2 [/latex]
• Pengagihan binomial dianggarkan dengan pengedaran normal di bawah keadaan tertentu tetapi tidak sebaliknya.