Perbezaan antara Laplace dan Fourier Transforms

Laplace vs Fourier Transforms
 

Kedua -dua Transformasi Laplace dan Transformasi Fourier adalah transformasi penting, yang paling biasa digunakan sebagai kaedah matematik untuk menyelesaikan sistem fizikal yang dimodelkan secara matematik. Prosesnya mudah. Model matematik yang kompleks ditukar kepada model yang lebih mudah dan mudah diselesaikan menggunakan transformasi integral. Sebaik sahaja model yang lebih mudah diselesaikan, transformasi integral songsang digunakan, yang akan memberikan penyelesaian kepada model asal.

Sebagai contoh, kerana kebanyakan sistem fizikal menghasilkan persamaan pembezaan, mereka boleh ditukar menjadi persamaan algebra atau persamaan pembezaan yang mudah diselesaikan dengan mudah menggunakan transformasi integral. Kemudian menyelesaikan masalah akan menjadi lebih mudah.

Apakah perubahan Laplace?

Diberi fungsi f (t) pemboleh ubah sebenar t, Transformasi Laplace ditakrifkan oleh integral [lateks] f (s) = \\ int_ 0^\\ infty e^-st f (t) dt [/lateks] (setiap kali ia wujud) adalah fungsi pemboleh ubah kompleks s. Biasanya dilambangkan oleh l f (t). Laplace songsang mengubah fungsi F(s) dianggap sebagai fungsi f (t) sedemikian rupa sehingga l f (t) = F(s), dan dalam notasi matematik yang biasa kita tulis, l ^-1F(s) = f (t).Transformasi songsang boleh dibuat unik jika fungsi null tidak dibenarkan. Seseorang dapat mengenal pasti kedua -dua pengendali linear yang ditakrifkan dalam ruang fungsi, dan juga mudah untuk melihatnya, l ^-1L f (t) = f (t), jika fungsi null tidak dibenarkan.

Jadual berikut menyenaraikan Laplace mengubah beberapa fungsi yang paling biasa.

Apakah transformasi Fourier?

Diberi fungsi f (t) pemboleh ubah sebenar t, Transformasi Laplace ditakrifkan oleh integral [latex] f (\\ alpha) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^i \\ alpha t f (t) dt [/latex] (setiap kali ia wujud), dan biasanya dilambangkan oleh f f (t). Transformasi songsang f ^-1F(α) diberikan oleh integral [latex] f (t) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^ -i \\ alpha t f (\\ alpha) d \\ alpha [/lateks]. Transformasi Fourier juga linear, dan boleh dianggap sebagai pengendali yang ditakrifkan dalam ruang fungsi.

Menggunakan transformasi Fourier, fungsi asal boleh ditulis seperti berikut dengan syarat fungsi itu hanya mempunyai bilangan ketidakselarasan yang terhingga dan benar -benar berintegrasi.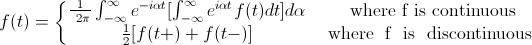

Apakah perbezaan antara Laplace dan Fourier Transforms?

• Transformasi Fourier Fungsi f (t) ditakrifkan sebagai [latex] f (\\ alpha) = \\ frac 1 \\ sqrt 2 \\ pi \\ int _ - \\ infty^\\ infty e^i i \\ alpha t f (t) dt [/latex], sedangkan transformasi Laplace itu ditakrifkan sebagai [latex] f (s) = \\ int_ 0^\\ infty e^-st f (t) dt [/lateks].
• Transformasi Fourier ditakrifkan hanya untuk fungsi yang ditakrifkan untuk semua nombor sebenar, sedangkan transformasi Laplace tidak memerlukan fungsi untuk ditakrifkan pada menetapkan nombor sebenar negatif.
• Transformasi Fourier adalah kes khas transformasi Laplace. Dapat dilihat bahawa kedua-duanya bertepatan dengan nombor sebenar yang tidak negatif. (i.e. ambil s di Laplace untuk menjadi Iα + β di mana α dan β sebenarnya seperti itu e ^β= ¹/_{√ (2ᴫ)})
• Setiap fungsi yang mempunyai transformasi Fourier akan mempunyai transformasi Laplace tetapi tidak sebaliknya.