Perbezaan antara hiperbola dan elips
Hyperbola vs Ellipse
Apabila kerucut dipotong pada sudut yang berbeza, lengkung yang berbeza ditandai dengan pinggir kon. Lengkung ini sering dipanggil bahagian kerucut. Lebih tepat lagi, seksyen konik adalah lengkung yang diperolehi dengan merentasi permukaan konik bulat yang betul dengan permukaan satah. Pada sudut persimpangan yang berbeza, bahagian konik yang berbeza diberikan.
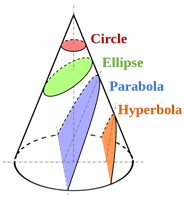
Kedua -dua hiperbola dan elips adalah bahagian kerucut, dan perbezaannya mudah dibandingkan dengan konteks ini.
Lebih banyak mengenai Ellipse
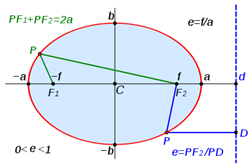
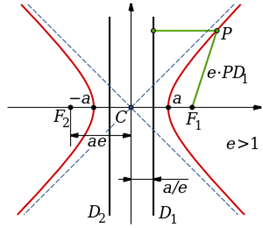
Apabila persimpangan permukaan konik dan permukaan satah menghasilkan lengkung tertutup, ia dikenali sebagai elips. Ia mempunyai sifat eksentrik antara sifar dan satu (0 Segmen garis yang melalui fokus dikenali sebagai paksi utama, dan paksi serenjang dengan paksi utama dan melalui pusat elips dikenali sebagai paksi kecil. Diameter di sepanjang setiap paksi dikenali sebagai diameter melintang dan diameter conjugate masing -masing. Separuh paksi utama dikenali sebagai paksi separuh utama, dan separuh daripada paksi kecil dikenali sebagai paksi separuh minor. Setiap titik f1 dan f2 dikenali sebagai fokus elips dan panjang F1 + Pf2 = 2a , di mana P adalah titik sewenang -wenangnya pada elips. Eksentrik e ditakrifkan sebagai nisbah antara jarak dari fokus ke titik sewenang -wenangnya ( Pf2 ) dan jarak tegak lurus ke titik sewenang -wenang dari directrix (PD). Ia juga sama dengan jarak antara kedua-dua fokus dan paksi separuh utama: e = PF/PD = f/a Persamaan umum elips, apabila paksi separuh utama dan paksi separuh minor bertepatan dengan paksi Cartesian, diberikan seperti berikut. x2/a2 + y2/b2 = 1 Geometri Ellipse mempunyai banyak aplikasi, terutamanya dalam Fizik. Orbit planet dalam sistem solar adalah elips dengan matahari sebagai satu tumpuan. Reflektor untuk peranti antena dan akustik dibuat dalam bentuk elips untuk memanfaatkan fakta bahawa sebarang pelepasan membentuk tumpuan akan menumpu pada fokus yang lain. Lebih banyak mengenai Hyperbola Hyperbola juga merupakan bahagian kerucut, tetapi ia terbuka berakhir. Istilah hiperbola dirujuk kepada dua lengkung terputus yang ditunjukkan dalam angka tersebut. Daripada menutup seperti elips lengan atau cawangan hiperbola terus ke tak terhingga. Titik di mana kedua -dua cawangan mempunyai jarak terpendek di antara mereka dikenali sebagai simpang. Garis yang melalui simpang dianggap sebagai paksi utama atau paksi melintang, dan ia adalah salah satu paksi utama hiperbola. Dua fokus parabola juga terletak pada paksi utama. Titik tengah garis antara kedua-dua simpang adalah pusat, dan panjang segmen garis adalah paksi separuh utama. Bisektor serenjang paksi separuh utama adalah paksi utama yang lain, dan dua lengkung hiperbola adalah simetri di sekitar paksi ini. Eksentrik parabola lebih besar daripada satu; e> 1. Sekiranya paksi utama bertepatan dengan paksi Cartesian, persamaan umum hiperbola adalah bentuk: x2/a2 - y2/b2 = 1, di mana a adalah paksi separuh utama dan b adalah jarak dari pusat sama ada fokus. Hiperbola dengan hujung terbuka menghadap paksi x dikenali sebagai hiperbola timur-barat. Hiperbola yang sama juga boleh didapati di paksi y. Ini dikenali sebagai hiperbola paksi y. Persamaan untuk hiperbola tersebut mengambil bentuk y2/a2 - x2/b2 = 1 Apakah perbezaan antara hiperbola dan elips? • Kedua -dua elips dan hiperbola adalah bahagian kerucut, tetapi elips adalah lengkung tertutup manakala hiperbola terdiri daripada dua lengkung terbuka. • Oleh itu, elips mempunyai perimeter terhingga, tetapi hiperbola mempunyai panjang tak terhingga. • Kedua -duanya adalah simetri di sekitar paksi utama dan kecil mereka, tetapi kedudukan Directrix adalah berbeza dalam setiap kes. Di Ellipse, ia terletak di luar paksi separa utama sementara, dalam hiperbola, ia terletak di paksi separuh utama. • Eksentrik kedua -dua bahagian konik berbeza. 0 eHyperbola > 0 • Persamaan umum kedua -dua lengkung kelihatan sama, tetapi mereka berbeza. • Bisektor tegak lurus dari paksi-paksi utama memotong lengkung di elips, tetapi tidak di hiperbola. (Imej Sumber: Wikipedia)