Perbezaan antara berlian, rombus dan trapezoid

Berlian, rombus vs trapezoid
 

Berlian, rombus, dan trapezoid semuanya Quadrilaterals, yang poligon dengan empat sisi. Walaupun rhombus dan trapezium ditakrifkan dengan betul dalam matematik, berlian (atau bentuk berlian) adalah istilah orang awam untuk rhombus.

Rhombus dan Diamond

Segi empat dengan semua sisi sama panjangnya dikenali sebagai rhombus. Ia juga dinamakan sebagai Quadrilateral sama. Ia dianggap mempunyai bentuk berlian, sama seperti yang ada di kad bermain. Bentuk Diamond bukan entiti geometri yang tepat.

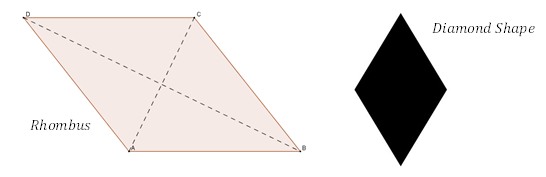
Rhombus adalah kes khas dari Parallelogram. Ia boleh dianggap sebagai selaras dengan sisi yang sama. Dataran boleh dianggap sebagai kes khas rombus, di mana sudut dalaman adalah sudut yang betul. Secara umum, rombus mempunyai sifat khas berikut

• Keempat -empat sisi adalah sama panjangnya. (AB = dc = ad = bc)

• pepenjuru rhombus bisect antara satu sama lain pada sudut tepat; Diagonal berserenjang antara satu sama lain,

Sebagai tambahan kepada sifat -sifat berikut selaras.

• Dua pasang sudut lawan adalah sama. (Dâb = bĉd, a ̂Dc = a ̂BC)

• Sudut bersebelahan adalah tambahan dâb+a ̂Dc = a ̂DC+B ̂Cd = b ̂CD+a ̂BC = a ̂BC+D ̂AB = 180 ° = π rad

• Sepasang sisi, yang menentang satu sama lain, selari dan sama panjangnya. (AB = DC & AB∥DC)

• Diagonal bisect antara satu sama lain (ao = oc, bo = od)

• Setiap pepenjuru membahagikan segi empat segi ke dua segi tiga kongruen. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)

• Pepenjuru membelah dua sudut dalaman yang bertentangan.

Kawasan rhombus boleh dikira menggunakan formula berikut.

Kawasan rhombus = ½ (ac × bd)

Trapezoid (trapezium)

Trapezoid adalah segi empat segi cembung di mana sekurang -kurangnya dua sisi selari dan tidak sama rata. Sisi selari trapezoid dikenali sebagai pangkalan dan kedua -dua pihak lain dipanggil kaki.

Berikut adalah ciri -ciri utama trapezoid;

• Sekiranya sudut bersebelahan tidak berada di pangkalan trapezoid yang sama, mereka adalah sudut tambahan. i.e. Mereka menambah sehingga 180 ° (BA ̂d+AD ̂C = AB ̂C+BC ̂d = 180 °)

• Dua pepenjuru trapezium bersilang pada nisbah yang sama (nisbah antara bahagian pepenjuru adalah sama).

• Sekiranya A dan B adalah pangkalan dan C, D adalah kaki, panjang pepenjuru diberikan oleh 

Kawasan trapezoid boleh dikira menggunakan formula berikut.

Membaca Perbezaan antara paralelogram dan trapezoid

Apakah perbezaan antara berlian, rombus dan trapezoid?

• Rhombus dan trapezoid adalah objek matematik yang jelas sementara bentuk berlian adalah istilah orang awam. Setiap bentuk mempunyai empat sisi, dan bentuk berlian merujuk kepada rhombus.

• Rhombus mempunyai sisi yang sama, dengan pihak lawan selari antara satu sama lain. Trapezoid mempunyai sisi yang tidak sama rata, dengan dua pihak selari antara satu sama lain. Hanya kaki trapezoid yang boleh sama.

• Sebarang pepenjuru rhombus memisahkan rombus menjadi dua segitiga kongruen. Segitiga yang dibentuk oleh pepenjuru trapezoid tidak semestinya kongruen.

• Diagonal rombus bersilang antara satu sama lain pada sudut tepat manakala pepenjuru trapezoid tidak semestinya berserenjang antara satu sama lain.

• Diagonal Rhombus bisect antara satu sama lain manakala pepenjuru rhombus bersilang pada nisbah yang sama.