Perbezaan antara circumcenter, insenter, orthocenter dan centroid

Circumcenter, insenter, ortocenter vs centroid

Circumcentier: circumcenter adalah titik persimpangan tiga bisektor tegak lurus segitiga. Circumcenter adalah pusat Circumcircle, yang merupakan bulatan melalui ketiga -tiga simpang segitiga.

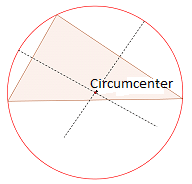
Untuk menarik circumcenter membuat mana -mana dua bisektor tegak lurus ke sisi segitiga. Titik persimpangan memberikan lingkaran. Bisektor boleh dibuat menggunakan kompas dan tepi lurus penguasa. Tetapkan kompas ke jejari, yang lebih daripada separuh panjang segmen garis. Kemudian buat dua arka di kedua -dua belah segmen dengan akhir sebagai pusat arka. Ulangi proses dengan hujung segmen yang lain. Empat arka membuat dua titik persimpangan di kedua -dua belah segmen. Lukiskan garis yang menyertai kedua -dua mata ini dengan bantuan penguasa, dan yang akan memberikan bisektor tegak lurus segmen.

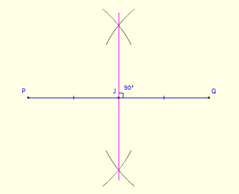
Untuk membuat circumcircle, lukis bulatan dengan circumcenter sebagai pusat dan panjang antara circumcenter dan puncak sebagai jejari bulatan.

Insenter: Insen adalah titik persimpangan ketiga -tiga sudut bisektors. Insen adalah pusat bulatan dengan lilitan bersilang ketiga -tiga sisi segitiga.

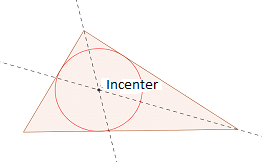
Untuk menarik insenter segitiga, buat dua dalaman Bisektor sudut segitiga. Titik persimpangan kedua -dua sudut bisektor memberikan insenter. Untuk menarik bisektor sudut, buat dua arka pada setiap lengan dengan jejari yang sama. Ini memberikan dua mata (satu pada setiap lengan) di lengan sudut. Kemudian mengambil setiap titik di lengan sebagai pusat, lukis dua lagi arka. Titik yang dibina oleh persimpangan kedua -dua arka ini memberikan titik ketiga. Garis yang menyertai puncak sudut dan titik ketiga memberikan sudut bisek.

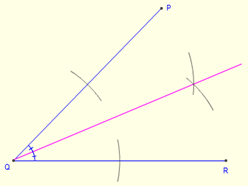
Untuk membuat tidak bulat, Bina segmen garis tegak lurus ke mana -mana sisi, yang melalui insenter. Mengambil panjang antara pangkal tegak lurus dan insenter sebagai jejari, lukis bulatan lengkap. 

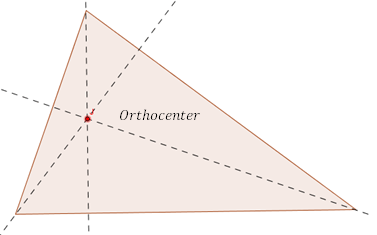
Orthocenter: Orthocenter adalah titik persimpangan tiga ketinggian (ketinggian) segitiga.

Untuk mencipta orthocenter, lukiskan dua ketinggian segitiga. Segmen garis tegak lurus ke sisi yang melewati puncak lawan dipanggil ketinggian. Untuk melukis garis tegak lurus melalui satu titik, pertama menandakan dua arka pada garisan dengan titik sebagai pusat. Kemudian, buat dua arka yang lain dengan setiap titik persimpangan sebagai pusat. Lukis segmen garis menyertai titik pertama dan titik akhirnya dibina, dan yang memberikan garis tegak lurus ke segmen garis dan melalui titik pertama. Titik persimpangan dua ketinggian memberikan orthocenter.

Centroid: Centroid adalah titik persimpangan ketiga -tiga median segitiga. Centroid membahagikan setiap median dalam nisbah 1: 2, dan pusat jisim seragam, lamina segi tiga terletak pada ketika ini.

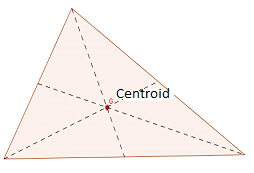
Untuk menentukan centroid, buat mana -mana dua median segitiga. Untuk membuat median, tandakan titik tengah sisi. Kemudian bina segmen garis yang menyertai titik tengah dan puncak lawan segitiga. Titik persimpangan median memberikan sentroid segitiga.

Apakah perbezaan di antara circumcenter, insenter, orthocenter dan centroid?

• Circumcenter dicipta menggunakan bisektor tegak lurus segitiga.

• Insenters dibuat menggunakan bisektor sudut segitiga.

• Orthocenter dicipta menggunakan ketinggian (ketinggian) segitiga.

• Centroid dicipta menggunakan median segitiga.

• Kedua -dua lingkaran dan insenter mempunyai lingkaran yang berkaitan dengan sifat geometri tertentu.

• Centroid adalah pusat geometri segitiga, dan ia adalah pusat jisim laminar segitiga seragam.

• Bagi segitiga yang tidak sama, circumcenter, orthocenter, dan centroid terletak pada garis lurus, dan garis itu dikenali sebagai Garis Euler.