Perbezaan antara paralelogram dan trapezoid

Parallelogram vs trapezoid
 

Paralelogram dan trapezoid (atau trapezium) adalah dua kuadrilatur cembung. Walaupun ini adalah quadrangles, geometri trapezoid berbeza dengan ketara dari paralelogram.

Parallelogram

Parallelogram boleh ditakrifkan sebagai angka geometri dengan empat sisi, dengan sisi bertentangan selari antara satu sama lain. Lebih tepatnya ia adalah segi empat segi dengan dua pasang sisi selari. Sifat selari ini memberikan banyak ciri geometri kepada selaras.

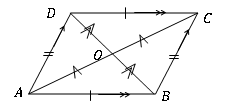
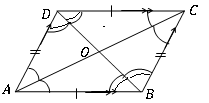
Duadrilateral adalah selaras dengan ciri -ciri geometri yang dijumpai.

• Dua pasang sisi lawan adalah sama panjangnya. (AB = DC, AD = BC)

• Dua pasang sudut lawan adalah sama. ([latex] d \ hat a b = b \ hat c d, a \ hat d c = a \ hat b c [/latex])

• Jika sudut bersebelahan adalah tambahan [lateks] d \ hat a b + a \ hat d c = a \ hat d c + b \ hat c d = b \ hat c d + A \ hat b c = a \ hat b c + d \ hat a b = 180^\ circ = \ pi rad [/latex]

• Sepasang sisi, yang menentang satu sama lain, selari dan sama panjangnya. (AB = DC & AB∥DC)

• Diagonal bisect antara satu sama lain (ao = oc, bo = od)

• Setiap pepenjuru membahagikan segi empat segi ke dua segi tiga kongruen. (ΔAdb ≡ ΔBcd, ΔABC ≡ ΔADC)

Selanjutnya, jumlah kuadrat di sisi sama dengan jumlah kuadrat diagonal. Ini kadang -kadang disebut sebagai Undang -undang Parallelogram dan mempunyai aplikasi yang meluas dalam fizik dan kejuruteraan. (AB² + BC² + CD² + Da² = Ac² + BD²)

Setiap ciri -ciri di atas boleh digunakan sebagai sifat, apabila ia ditetapkan bahawa kuadrilateral adalah selaras.

Kawasan paralelogram boleh dikira dengan produk panjang satu sisi dan ketinggian ke seberang. Oleh itu, kawasan selaras boleh dinyatakan sebagai

Kawasan paralelogram = asas × ketinggian = Ab×h

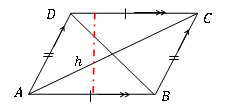
Kawasan paralelogram bebas daripada bentuk parallelogram individu. Ia hanya bergantung pada panjang asas dan ketinggian tegak lurus.

Sekiranya sisi paralelogram boleh diwakili oleh dua vektor, kawasan ini boleh diperolehi dengan magnitud produk vektor (produk silang) dari dua vektor bersebelahan.

Jika sisi AB dan AD diwakili oleh vektor ([latex] \ overrightarrow ab [/latex]) dan ([latex] \ overrightarrow ad [/lateks]) masing -masing, kawasan parallelogram diberikan oleh [ lateks] \ kiri | \ overrightarrow ab \ times \ overrightarrow ad \ right | = Ab \ cdot ad \ sin \ alpha [/latex], di mana α adalah sudut antara [latex] \ overrightarrow ab [/latex] dan [latex] \ overrightarrow ad [/latex]. 

Berikut adalah beberapa sifat lanjutan dari paralelogram;

• Kawasan paralelogram adalah dua kali ganda kawasan segitiga yang dicipta oleh mana -mana pepenjuru.

• Kawasan paralelogram dibahagikan kepada separuh oleh mana -mana garis yang melalui titik tengah.

• Sebarang transformasi affine yang tidak merosakkan mengambil selaras dengan selaras yang lain

• Parallelogram mempunyai simetri putaran pesanan 2

• Jumlah jarak dari mana -mana titik pedalaman dari paralelogram ke sisi adalah bebas dari lokasi titik

Trapezoid

Trapezoid (atau Trapezium dalam bahasa Inggeris Inggeris) adalah kuadrilateral cembung di mana sekurang -kurangnya dua sisi selari dan tidak sama rata. Sisi selari trapezoid dikenali sebagai pangkalan dan dua sisi lain dipanggil kaki.

Berikut adalah ciri -ciri utama trapezoid;

• Jika sudut bersebelahan tidak berada di pangkalan trapezoid yang sama, mereka adalah sudut tambahan. i.e. Mereka menambah sehingga 180 ° ([latex] b \ hat a d+a \ hat d c = a \ hat b c+b \ hat c d = 180^\ circ [/ lateks])

• Kedua -dua pepenjuru trapezium bersilang pada nisbah yang sama (nisbah antara bahagian pepenjuru adalah sama).

• Sekiranya A dan B adalah pangkalan dan C, D adalah kaki, panjang pepenjuru diberikan oleh  

[latex] \ sqrt \ frac ab^2 -a^2 b-ac^2+bd^2 b-a [/latex] 

dan

[latex] \ sqrt \ frac ab^2 -a^2 b-ac^2+bc^2 b-a [/latex]

Kawasan trapezoid boleh dikira menggunakan formula berikut

Kawasan trapezoid = [latex] \ frac a+b 2 \ times h [/latex]

Apakah perbezaan antara paralelogram dan trapezoid (trapezium)?

• Kedua -dua paralelogram dan trapezoid adalah quadrilaterals cembung.

• Dalam selaras, kedua -dua pasang pihak lawan selari sementara, dalam trapezoid, hanya sepasang selari.

• Diagonal dari paralelogram bisect antara satu sama lain (nisbah 1: 1) manakala pepenjuru trapezoid bersilang dengan nisbah malar antara bahagian -bahagian.

• Kawasan paralelogram bergantung pada ketinggian dan pangkalan sementara kawasan trapezoid bergantung pada ketinggian dan segmen pertengahan.

• Kedua -dua segitiga yang dibentuk oleh pepenjuru dalam paralelogram sentiasa kongruen manakala segitiga trapezoid boleh menjadi kongruen atau tidak.