Perbezaan antara graf yang diarahkan dan tidak diarahkan

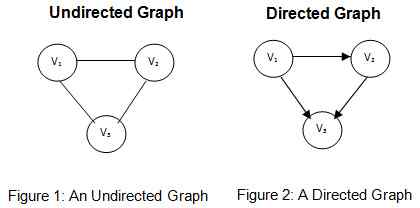
Diarahkan vs graf yang tidak diarahkan

Grafik adalah struktur matematik yang terdiri daripada set simpang dan tepi. Grafik mewakili satu set objek (diwakili oleh simpang) yang disambungkan melalui beberapa pautan (diwakili oleh tepi). Menggunakan notasi matematik, graf boleh diwakili oleh g, di mana g = (v, e) dan v adalah set simpang dan e adalah set tepi. Dalam graf yang tidak diarahkan tidak ada arah yang berkaitan dengan tepi yang menyambungkan simpul. Dalam graf yang diarahkan terdapat arah yang berkaitan dengan tepi yang menyambungkan simpul.

Graf yang tidak diarahkan

Seperti yang dinyatakan sebelum ini, graf yang tidak diarahkan adalah graf di mana tidak ada arah di tepi yang menghubungkan simpul dalam graf. Rajah 1 menggambarkan graf yang tidak diarahkan dengan set simpang v = v1, v2, v3. Set tepi dalam graf di atas boleh ditulis sebagai v = (v1, v2), (v2, v3), (v1, v3). Ia juga boleh diperhatikan bahawa tidak ada yang menghalang menulis set tepi sebagai v = (v2, v1), (v3, v2), (v3, v1) ​​kerana tepi tidak mempunyai arah. Oleh itu tepi dalam graf yang tidak diarahkan tidak dipesan pasangan. Ini adalah ciri utama graf yang tidak diarahkan. Grafik yang tidak diarahkan boleh digunakan untuk mewakili hubungan simetri antara objek yang diwakili oleh simpang. Sebagai contoh, rangkaian jalan dua jalan yang menghubungkan satu set bandar boleh diwakili menggunakan graf yang tidak diarahkan. Bandar -bandar boleh diwakili oleh simpang dalam graf dan tepi mewakili jalan dua cara yang menghubungkan bandar.

Graf yang diarahkan

Grafik yang diarahkan adalah graf di mana tepi dalam graf yang menghubungkan simpang mempunyai arah. Rajah 2 menggambarkan graf yang diarahkan dengan set simpang v = v1, v2, v3. Set tepi dalam graf di atas boleh ditulis sebagai v = (v1, v2), (v2, v3), (v1, v3). Tepi dalam graf yang tidak diarahkan dipesan pasangan. Secara rasmi, kelebihan e dalam graf yang diarahkan boleh diwakili oleh pasangan yang diperintahkan e = (x, y) di mana x adalah puncak yang dipanggil asal, sumber atau titik awal kelebihan e, dan puncak y dipanggil terminal , menamatkan titik puncak atau terminal. Sebagai contoh, rangkaian jalan yang menghubungkan satu set bandar menggunakan satu cara jalan boleh diwakili menggunakan graf yang tidak diarahkan. Bandar -bandar boleh diwakili oleh simpang dalam graf dan tepi yang diarahkan mewakili jalan -jalan yang menghubungkan bandar -bandar memandangkan arah lalu lintas mengalir di jalan raya.

Apakah perbezaan antara graf yang diarahkan dan graf yang tidak diarahkan?

Dalam graf yang diarahkan kelebihan adalah pasangan yang diperintahkan, di mana pasangan yang diperintahkan mewakili arah tepi yang menghubungkan kedua -dua simpul. Sebaliknya, dalam graf yang tidak diarahkan, kelebihan adalah pasangan yang tidak teratur, kerana tidak ada arah yang berkaitan dengan kelebihan. Grafik yang tidak diarahkan boleh digunakan untuk mewakili hubungan simetri antara objek. Dalam darjah dan darjah setiap nod dalam graf yang tidak diarahkan adalah sama tetapi ini tidak benar untuk graf yang diarahkan. Apabila menggunakan matriks untuk mewakili graf yang tidak diarahkan, matriks selalu menjadi graf simetri, tetapi ini tidak benar untuk graf yang diarahkan. Grafik yang tidak diarahkan boleh ditukar kepada graf yang diarahkan dengan menggantikan setiap kelebihan dengan dua tepi yang diarahkan ke arah yang bertentangan. Walau bagaimanapun, tidak mungkin untuk menukar graf yang diarahkan ke graf yang tidak diarahkan.