Perbezaan antara koordinat Cartesian dan koordinat kutub
Koordinat Cartesian vs koordinat kutub
Dalam geometri, sistem koordinat adalah sistem rujukan, di mana nombor (atau koordinat) digunakan untuk secara unik menentukan kedudukan titik atau elemen geometri lain di ruang angkasa. Sistem koordinat membolehkan masalah geometri ditukar menjadi masalah berangka, yang menyediakan asas untuk geometri analitik.
Sistem koordinat Cartesian dan sistem koordinat kutub adalah dua sistem koordinat biasa yang digunakan dalam matematik.
Koordinat Cartesian
Sistem koordinat Cartesian menggunakan garis nombor sebenar sebagai rujukan. Dalam satu dimensi, garisan nombor meluas dari infiniti negatif ke infiniti positif. Memandangkan titik 0 sebagai permulaan, panjang ke setiap titik dapat diukur. Ini memberikan cara yang unik untuk mengenal pasti kedudukan pada baris, dengan satu nombor.
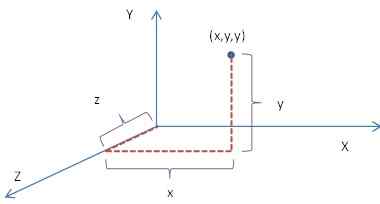
Konsep ini dapat dilanjutkan ke dalam dua dan tiga dimensi di mana garis bilangan berserenjang antara satu sama lain digunakan. Mereka semua berkongsi titik yang sama 0 sebagai permulaan. Garis nombor disebut sebagai paksi, dan sering dipanggil paksi x, paksi y, dan paksi z. Jarak ke titik di sepanjang setiap paksi bermula dari (0, 0, 0), yang juga dikenali sebagai asal, dan diberikan sebagai tuple dikenali sebagai koordinat titik. Titik umum dalam ruang ini boleh diwakili oleh koordinat (x, y, z). Dalam sistem kapal terbang di mana terdapat hanya dua paksi, koordinat diberikan sebagai (x, y). Satah yang dibuat oleh paksi dikenali sebagai satah Cartesian, dan sering dirujuk oleh huruf paksi. E.g. XY Plane.

Titik umum ini dapat digunakan untuk menggambarkan unsur -unsur geometri yang berbeza dengan menghalang titik umum untuk berkelakuan dengan cara tertentu. Sebagai contoh, Persamaan X^2+Y^2 = A^2 mewakili bulatan. Daripada melukis bulatan dengan jejari A, mungkin untuk menunjukkan bulatan dengan cara yang lebih abstrak yang ditunjukkan di atas.
Koordinat kutub
Koordinat Polar Gunakan sistem rujukan perbezaan untuk menunjukkan titik. Sistem koordinat kutub menggunakan kaunter jam mengikut arah jam dari arah positif paksi x dan jarak garis lurus ke titik sebagai koordinat.
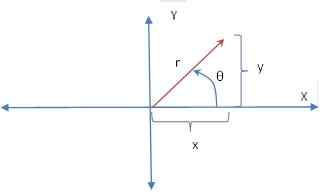
Koordinat kutub boleh diwakili seperti di atas dalam sistem koordinat Cartesian dua dimensi.
Transformasi antara sistem kutub dan Cartesian diberikan dengan mengikuti hubungan:
r = √ (x2 + y2) ↔ x = r cosθ, y = r sinθ
θ = tan-1 (x/y)
Apakah perbezaan antara koordinat Cartesian dan Polar?
• Koordinat Cartesian menggunakan garisan nombor sebagai paksi, dan ia boleh digunakan dalam satu, dua atau tiga dimensi. Oleh itu mempunyai keupayaan untuk mewakili geometri linear, planar, dan pepejal.
• Koordinat kutub menggunakan sudut dan panjang sebagai koordinat, dan ia hanya boleh mewakili geometri linear dan planar, walaupun ia boleh dibangunkan menjadi sistem koordinat silinder, untuk mewakili geometri pepejal.
• Kedua -dua sistem digunakan untuk mewakili nombor khayalan dengan menentukan paksi khayalan, dan memainkan peranan penting dalam aljabar kompleks. Walaupun, dalam bentuk biasa, koordinat Cartesian adalah nombor nyata (x, y, z) koordinat dalam sistem kutub tidak selalu angka nyata; i.e. Jika sudut diberikan dalam darjah, koordinat tidak nyata; Sekiranya sudut diberikan dalam koordinat radian adalah nombor sebenar.